在宇宙的宏觀圖景裡,有些圖案憑藉其簡明卻深刻的普遍性,橫跨數學、自然、藝術甚至金融領域。斐波那契數列就是這樣一個迷人的數學奇觀。它不僅勾勒出從花朵瓣數到銀河漩渦的自然法則,還在當代科技與股市分析中發揮樞紐作用。這篇文章將引領您深入探討斐波那契數列的奧妙,從它古老的起源,到與黃金比例的密切連結,再到在自然、程式設計以及金融交易上的多樣運用。您準備好揭開這串連結宇宙秩序與人類洞察的黃金密碼了嗎?讓我們一起啟程,展開這場探索之旅。

## 斐波那契數列是什麼?起源故事與基本定義
斐波那契數列看起來簡單,卻蘊含無盡的深層意涵。它的基本規則是,從第三項起,每一項數字都來自前兩項的相加。這組序列最早由中世紀義大利數學家列奧納多·斐波那契(約1170–1250年)在《計算之書》中引介到西方世界。
斐波那契其實不是這數列的創造者,他只是讓它廣為人知。他用一個著名的兔子繁殖謎題來說明:想像一對初生兔子(一公一母),它們出生一個月後成熟,第二個月起每月產下一對小兔。如果兔子永遠不死,一年內會有多少對?這個謎題的解答正好形成了斐波那契數列:
– 第一個月:1對(新生)
– 第二個月:1對(成熟)
– 第三個月:2對(原對生出一對)
– 第四個月:3對(原對再產,新生對成熟)
– 第五個月:5對
依此類推,前幾項常從0或1起頭,序列為:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144……

### 斐波那契數列的遞迴公式與初始條件
要真正把握斐波那契數列,就得從它優雅的遞迴公式入手,這公式清楚描述了每一項與前兩項的關聯。
**遞迴公式:**
$F(n) = F(n-1) + F(n-2)$
這裡:
– $F(n)$ 是數列第$n$項。
– $F(n-1)$ 是第$n-1$項。
– $F(n-2)$ 是第$n-2$項。
**初始條件:**
斐波那契數列的起點有兩種主流設定,這會略微改變前幾項,但遞迴本質相同:
1. **從0開始的標準版:**
$F(0) = 0$
$F(1) = 1$
序列即:0, 1, 1, 2, 3, 5, 8, 13, 21, 34……
2. **從1開始的另一版:**
$F(1) = 1$
$F(2) = 1$
序列即:1, 1, 2, 3, 5, 8, 13, 21, 34……
兩種在學術與實務中都通用,只要註明起點即可。舉例來說,用$F(0)=0, F(1)=1$起算:
– $F(2) = F(1) + F(0) = 1 + 0 = 1$
– $F(3) = F(2) + F(1) = 1 + 1 = 2$
– $F(4) = F(3) + F(2) = 2 + 1 = 3$
– $F(5) = F(4) + F(3) = 3 + 2 = 5$
這樣一步步,就能無限延伸出任意項。這種生成方式不僅簡易,還能延伸到更複雜的數學應用,如生成函數或矩陣表示,讓數列計算更高效。
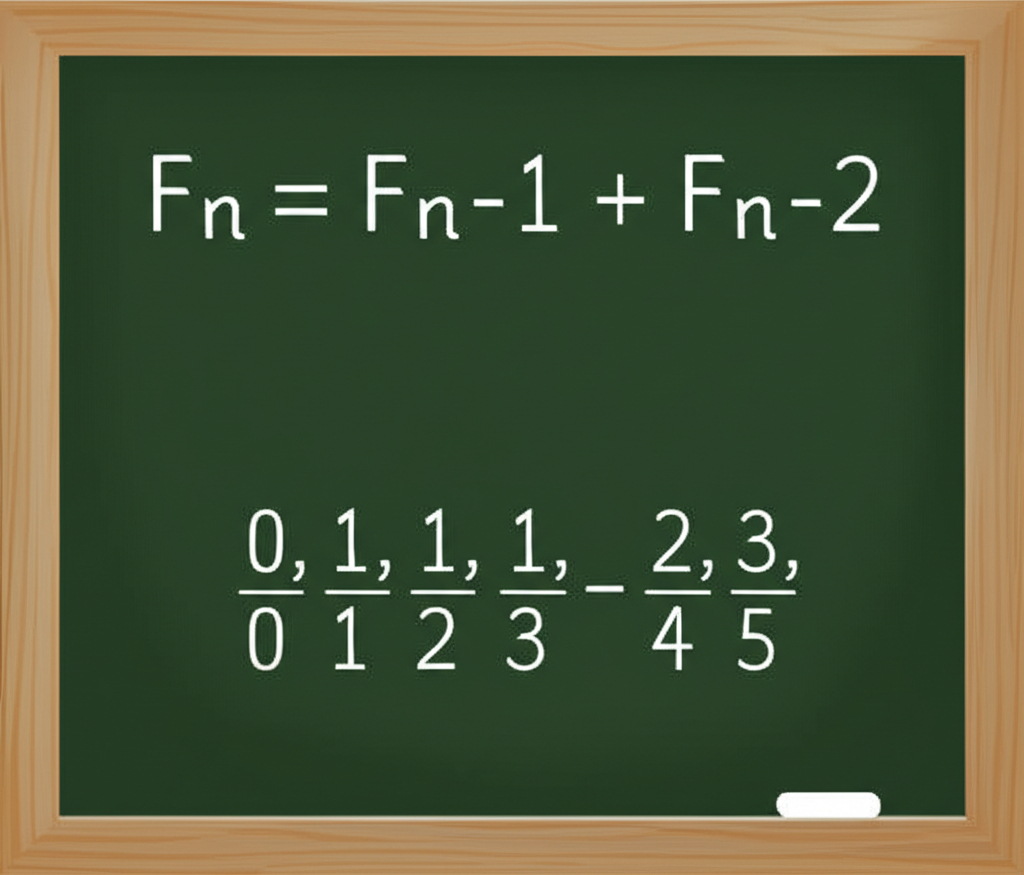
## 黃金比例:斐波那契數列的自然夥伴
黃金比例,用希臘字母φ表示,值約1.6180339887……,從古時起就被當作美的化身,廣泛見於藝術、建築與自然界。它與斐波那契數列的連結如此緊密,讓人驚嘆。
隨著斐波那契數列數字增大,相鄰兩項的比率會逐步逼近黃金比例。比方說:
– 3/2 = 1.5
– 5/3 ≈ 1.666
– 8/5 = 1.6
– 13/8 = 1.625
– 21/13 ≈ 1.615
– 34/21 ≈ 1.619
項數越多,這比率越貼近1.6180339887……,一個無限不循環的無理數,卻帶來強烈的和諧美感。
黃金比例不只數字,更是結構指南。當矩形長寬比達黃金比例,就成黃金矩形。从中切出正方形,剩餘部分仍是黃金矩形。重複此步並畫上四分之一圓弧,即形成黃金螺旋。這螺旋視覺上流暢自然,在大自然中屢見不鮮,完美詮釋斐波那契數列與黃金比例的美學融合。事實上,這種結構不僅限於視覺,還影響生物生長模式,如葉片排列的最佳角度(約137.5度,源自黃金比例),幫助植物捕捉最多陽光。
## 斐波那契數列在自然界中的奇妙體現
斐波那契數列與黃金比例的魅力,在於它們從抽象數學轉化為周遭世界的真實圖景。從細微植物到浩瀚星系,這模式彷彿是大自然的基本藍圖,無處不在。
### 植物世界的斐波那契模式
植物界是這些圖案最生動的展現場域。
– **向日葵種子排列**:花盤上種子螺旋排列,螺旋數常為斐波那契數字,如34與55,或55與89。這些螺旋雙向交錯,比率近黃金比例,如此設計讓空間利用極致化,容納更多種子。
– **松果鱗片**:鱗片螺旋數通常是5與8,或8與13,展現高效的生長效率。
– **鳳梨果實紋路**:表面塊狀螺旋,同樣對應相鄰斐波那契數字,確保果實緊密包覆。
– **樹枝分岔**:許多樹種的分枝遵循此序列,主幹分出一枝,那枝再分,逐步對應斐波那契成長,優化養分分配。
– **花瓣數量**:花瓣常為斐波那契數字,如百合3片、毛茛5片、飛燕草8片、金盞花13片、雛菊21片、紫菀34、55或89片。這是進化結果,助於光照與保護的最佳化。
這些例子顯示,斐波那契不僅美觀,還具功能性,如在葉序(phyllotaxis)中避免重疊,最大化資源。
### 動物與生物結構的黃金分割
這種模式也滲透動物與人類結構:
– **鸚鵡螺殼的螺旋生長**:殼體擴張成對數螺旋,每室比前一室大固定比率,近似黃金螺旋,體現自然精準美。
– **蜂巢結構**:雖以六邊形為主,但蜂群增長與比例有時呼應斐波那契,如工蜂與雄蜂數的動態。
– **人類身體比例**:達文西的《維特魯威人》捕捉人體黃金分割,如肚臍分上下比值近φ;手指骨、臉部五官也常以此為準。美國國家醫學圖書館研究顯示,這比例在面部美學中影響吸引力認知,根植生物本能。您可以參考 National Library of Medicine 了解更多。實際上,這不僅限歷史藝術,還延伸到現代整形與設計,強化視覺和諧。
## 斐波那契數列在現代領域的實用應用與深度解析
斐波那契數列的價值遠超自然美學,它在當代科技、金融與藝術中提供實用工具,凸顯跨界潛力。
### 金融市場分析:斐波那契回撤與擴展實戰
在交易圈,斐波那契工具是技術分析的利器,依賴數列與黃金比例,辨識支撐、阻力與目標。
* **斐波那契回撤(Fibonacci Retracement)的原理**:
這方法預測趨勢中價格回調位。資產大漲或大跌後,常在特定比率停頓,視為支撐(漲勢)或阻力(跌勢)。
* **關鍵回撤水平**:常見23.6%、38.2%、50%、61.8%、78.6%。38.2%與61.8%最關鍵,源自黃金比例;50%雖非斐波那契,卻是心理關卡。
* **繪製與解讀**:選定趨勢區(如低點到高點),軟體自動標線。價格觸及這些位,可能反轉。
* 例如,漲勢回調至38.2%或61.8%後續漲,即買入機會。實務中,這常與成交量結合,增強信號可靠性。
* **斐波那契擴展(Fibonacci Extension)的原理**:
用於突破後預測目標,設利潤點或延伸範圍。
* **關鍵擴展水平**:123.6%、138.2%、150%、161.8%、200%、261.8%。
* **繪製與解讀**:用三點:趨勢起、終、回調末。計算未來位。
* 例如,回調後破高,161.8%可作獲利目標。在波段交易,這幫助鎖定多頭潛力。
* **K線圖示範與實戰**:
(此處應插入一張 K 線圖,示範如何在上升趨勢中繪製斐波那契回撤線,並標註關鍵回撤水平,以及在突破後繪製斐波那契擴展線,標註潛在目標位。圖片需清晰展示工具的應用步驟。)
**步驟教學**:
1. **識別趨勢**:在K線圖找明顯漲跌。
2. **選擇工具**:選「斐波那契回撤」。
3. **繪製回撤**:漲勢從低點(0%)拉到高點(100%);跌勢反之。
4. **觀察反應**:看價格在水平位反轉或整。
5. **繪製擴展(若適用)**:選「斐波那契擴展」,點起、終、回調點,預測目標。
* **局限性與風險**:
這些工具雖流行,但非絕對。市場多變,受多因素影響。宜配其他指標如移動平均、RSI、MACD及基本面,並嚴控風險。Investopedia指出,斐波那契回撤僅為確認工具,非唯一依據。您可參考 Investopedia – Fibonacci Retracement 了解更多。舉例,在波動市,假突破常見,需止損保護。
### 程式設計與演算法實現詳解
斐波那契數列是程式入門的經典,示範遞迴、迭代與動態規劃。
* **遞迴(Recursion)實現**:
遞迴讓函數自呼,公式直譯成碼。
“`python
def fibonacci_recursive(n):
if n <= 1:
return n
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
```
* **優點**:碼短、直觀。
* **缺點**:重算多,時間O(2^n),大n慢。適合小n示範。
* **迭代(Iteration)實現**:
用迴圈避重算,高效。
```python
def fibonacci_iterative(n):
if n <= 1:
return n
a, b = 0, 1
for _ in range(2, n + 1):
a, b = b, a + b
return b
```
* **優點**:O(n)時間,O(1)空間,實用。
* **缺點**:不如遞迴詩意,但易懂。在大數據,這是首選。
* **動態規劃(Dynamic Programming)優化**:
存中間結果避重算。迭代即底層DP;記憶化為頂層。
```python
# 記憶化 (Top-down Dynamic Programming)
memo = {}
def fibonacci_dp_memo(n):
if n <= 1:
return n
if n in memo:
return memo[n]
memo[n] = fibonacci_dp_memo(n-1) + fibonacci_dp_memo(n-2)
return memo[n]
```
* **優點**:O(n)時間,清晰高效。
* **應用**:擴及路徑優化等複雜題。這在AI與遊戲開發中關鍵。
### 藝術、建築與設計中的斐波那契美學
黃金比例與斐波那契在藝術建築中,證明數學即美源。
- **古希臘**:帕德嫩神廟比例融黃金分割,營造莊嚴平衡。
- **文藝復興**:達文西、米開朗基羅用之於畫雕,如《蒙娜麗莎》與《最後的晚餐》構圖,達視覺完美。
- **現代設計**:平面、網頁、產品用黃金比例排版,提升吸引力。如App介面按鈕佈局,優化體驗。紐約時報文章討論蘋果標誌爭議,凸顯其影響。您可參考 The New York Times – The Golden Ratio 了解更多。在UI/UX,這比例減認知負荷,增用戶黏著。
## 結論:斐波那契數列的無限魅力與未來展望
斐波那契數列,這簡單遞迴序列,影響深遠。它是數學瑰寶,更是連結自然、藝術、科學與科技的紐帶。从兔子謎題到向日葵螺旋,從股市預測到碼優化,它無所不在,揭示宇宙韻律與美。
這黃金密碼教我們,深奧真理常藏簡樸形式。掌握它,不只加深數學認知,還激發新視野,發掘日常規律。隨科技躍進與跨域研究,斐波那契與黃金比例將續在發現、創新、美學中發光,驅動我們探未知。
## 常見問題 (FAQ)
斐波那契數列與黃金比例之間有什麼具體關聯?
當斐波那契數列中的數字越大,相鄰兩項的比值(例如 $F(n) / F(n-1)$)就越會趨近於一個定值,這個定值就是黃金比例(約 1.618)。例如,$34/21 \approx 1.619$,而 $89/55 \approx 1.618$。這種趨近關係是兩者之間最核心的數學關聯。
在股票或外匯市場中,斐波那契回撤線應該如何正確繪製和解讀?
要正確繪製斐波那契回撤線:
- **上升趨勢**:從趨勢的最低點(作為 0% 水平)拖曳到最高點(作為 100% 水平)。
- **下降趨勢**:從趨勢的最高點(作為 0% 水平)拖曳到最低點(作為 100% 水平)。
解讀時,這些回撤水平(如 23.6%、38.2%、50%、61.8%、78.6%)被視為潛在的支撐位(在上升趨勢回調時)或阻力位(在下降趨勢反彈時)。價格在這些水平附近可能出現反轉或盤整。但請注意,應結合其他技術指標綜合判斷。
斐波那契數列除了在自然界中,還可以在哪些領域找到應用?
除了自然界,斐波那契數列在現代社會中也有廣泛應用:
- **金融市場**:用於技術分析,如斐波那契回撤、擴展和扇形線,預測價格走勢和目標。
- **程式設計**:作為演算法教學(遞迴、迭代、動態規劃)的經典範例,也用於數據結構和演算法優化。
- **藝術與建築**:設計師和藝術家利用黃金比例創造視覺和諧與平衡,如古希臘建築、文藝復興繪畫和現代設計。
- **音樂**:一些作曲家在樂曲結構、節奏和和聲中使用斐波那契數列來實現平衡感。
有沒有簡單的記憶方法可以快速理解斐波那契數列的生成規則?
最簡單的記憶方法就是記住它的核心規則:「**前兩項之和,等於下一項**」。
您只需記住最開始的兩項(例如 0 和 1),然後就可以無限生成下去:
- 0 + 1 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
透過不斷重複這個加法動作,就能輕鬆記住和生成整個數列。
斐波那契數列的遞迴公式是什麼,以及如何用程式碼實現它?
斐波那契數列的遞迴公式是:$F(n) = F(n-1) + F(n-2)$,其中 $F(0)=0, F(1)=1$(或 $F(1)=1, F(2)=1$)。
用 Python 程式碼實現遞迴方法如下:
def fibonacci_recursive(n):
if n <= 1:
return n
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
但請注意,遞迴方法效率較低,對於較大的 $n$ 值,迭代或動態規劃會是更好的選擇。
斐波那契數列中,為什麼常見的起始項會有 0, 1, 1 和 1, 1, 2 兩種不同說法?
這兩種說法都廣為接受,主要取決於定義的習慣和應用場景:
- **0, 1, 1, 2... (F(0)=0, F(1)=1)**:這是最常見的數學定義,尤其在電腦科學和演算法分析中更為流行,因為它簡潔地包含了 0。
- **1, 1, 2, 3... (F(1)=1, F(2)=1)**:這種定義更接近斐波那契最初提出的「兔子問題」的語境,因為兔子數量不可能為 0。在某些數學和歷史文獻中也常使用。
雖然起始項不同,但從第三項(或第四項,取決於定義)開始,數列的序列是相同的,核心的遞迴關係也保持不變。
斐波那契數列的數字總和有什麼特殊的數學性質嗎?
是的,斐波那契數列的總和具有一些有趣的性質。其中一個著名的恆等式是:
斐波那契數列前 n 項的總和等於第 (n+2) 項減 1。
用公式表示為:$\sum_{i=0}^{n} F(i) = F(n+2) - 1$
例如,數列前 5 項之和 ($F(0)$ 到 $F(4)$):$0+1+1+2+3 = 7$。根據公式,$F(4+2)-1 = F(6)-1 = 8-1 = 7$。這個性質在數學證明和某些演算法分析中很有用。
在日常生活中,我們還能在哪裡觀察到斐波那契數列或黃金比例的蹤影?
斐波那契數列和黃金比例的蹤影比您想像的更為普遍:
- **信用卡或身份證**:許多卡片的長寬比例接近黃金比例。
- **書籍封面或照片構圖**:攝影師和設計師常使用黃金分割來構圖,使畫面更具平衡感和吸引力。
- **音樂樂器**:小提琴等樂器的某些部件比例可能與黃金比例有關。
- **星系和颶風**:螺旋星系和颶風的形狀有時被認為近似於黃金螺旋。
- **人體**:除了達文西的維特魯威人,人體許多部位的比例,如從肩膀到指尖與手肘到指尖的比例,也常被提及與黃金比例相關。
斐波那契擴展 (Fibonacci Extension) 是什麼,它和斐波那契回撤有何不同?
斐波那契擴展和回撤都是基於斐波那契比例的技術分析工具,但它們的用途不同:
- **斐波那契回撤 (Retracement)**:用於識別市場在經歷一段趨勢後,可能回調的潛在支撐或阻力水平。它主要幫助交易者判斷趨勢中的「休息點」。
- **斐波那契擴展 (Extension)**:用於預測價格在突破前高(或前低)後,可能達到的潛在利潤目標或趨勢延伸的水平。它主要幫助交易者判斷趨勢的「未來去向」。
簡而言之,回撤看的是「回頭路」,擴展看的是「向前路」。兩者結合使用可以為交易者提供更全面的市場分析視角。
學習斐波那契數列對於理解其他數學概念有什麼幫助?
學習斐波那契數列是理解許多其他數學和科學概念的絕佳起點:
- **遞迴與迭代**:它是學習這兩種基本演算法思維最直觀的例子。
- **動態規劃**:透過斐波那契數列的優化,能深入理解如何避免重複計算,提升演算法效率。
- **黃金比例**:兩者緊密相連,理解斐波那契數列有助於掌握黃金比例在數學、幾何、藝術中的重要性。
- **數論**:斐波那契數列本身就是數論的一個分支,引出許多有趣的恆等式和性質。
- **自然模式與碎形**:它揭示了自然界中重複和自相似的模式,有助於理解碎形幾何和混沌理論。
- **線性代數**:斐波那契數列也能透過矩陣運算來高效計算,涉及線性代數概念。
總之,斐波那契數列是一個多功能且啟發性的數學工具,能夠打開通往廣闊數學世界的大門。