費波那契數列：黃金比例、金融交易、程式設計，5大領域的應用與解析

非波那契數列是什麼？起源與基本定義

在數學的廣闊世界中，有一個看似簡單卻無處不在的數列，深深影響著自然、藝術、科技與市場——它就是非波那契數列。這個數列最早由13世紀義大利數學家李奧納多·非波那契（Leonardo Fibonacci）在其著作《計算之書》（Liber Abaci）中提出，當時他用一個關於兔子繁殖的假想問題，向歐洲介紹了印度－阿拉伯數字系統，也無意間揭開了一個數學奇蹟的序幕：假設一對兔子每月生一對新兔，新生兔在第二個月起也能繁殖，那麼經過若干個月後，兔子的總對數會依循特定規律增長，這正是非波那契數列的雛形。

這個數列的結構極為簡潔：從第三項開始，每一項都等於前兩項之和。數學上可表示為 $F_n = F_{n-1} + F_{n-2}$。通常以 $F_0 = 0$、$F_1 = 1$ 為起始，由此展開的數列為：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……這個序列不僅僅是數學課本中的練習題，更是一把打開自然與人工系統背後規律的鑰匙。從花瓣的數量到星系的旋臂，從演算法設計到市場波動，它的身影無所不在。

費波那契數列的公式與遞推關係詳解

非波那契數列的核心在於其遞推特性。只要知道前兩項的值，就能一步步推導出後續所有數字。以 $F_0 = 0$ 和 $F_1 = 1$ 為基礎：

– $F_2 = F_1 + F_0 = 1 + 0 = 1$
– $F_3 = F_2 + F_1 = 1 + 1 = 2$
– $F_4 = F_3 + F_2 = 2 + 1 = 3$
– $F_5 = F_4 + F_3 = 3 + 2 = 5$

如此反覆運算，數列便無限延伸。這種遞推方式直觀且易於理解，特別適合用於教學或初步建模。然而，當需要快速取得數列中某一特定項時，逐項計算顯得效率低下。這時，數學家提出了更高效的解法——比內公式（Binet’s formula）。

比內公式提供了一種直接計算 $F_n$ 的閉合形式，無需依賴前項：

$$
F_n = \frac{\phi^n – (-\phi)^{-n}}{\sqrt{5}}, \quad \text{其中 } \phi = \frac{1 + \sqrt{5}}{2}
$$

這個公式中的 $\phi$ 正是著名的黃金比例。儘管涉及無理數與指數運算，理論上可精確求值，但在實際應用中，特別是電腦程式設計，浮點數精度問題可能導致誤差。因此，多數工程與金融場景仍偏好使用遞推或迭代方法，確保計算穩定與效率兼顧。

黃金比例與費波那契數列的奧秘關聯

若僅將非波那契數列視為一串數字，便錯失了其最迷人的本質——它與黃金比例之間的深刻連結。黃金比例，符號為 $\phi$（Phi），約等於 1.6180339887……，是一個無理數，擁有獨特的數學性質：它等於自身的倒數加一（即 $\phi = 1 + \frac{1}{\phi}$）。而這個神秘數字，正隱藏在非波那契數列的比值之中。

當我們計算數列中相鄰兩項的比值 $\frac{F_n}{F_{n-1}}$，會發現這個值隨著 $n$ 增大而逐漸逼近 $\phi$：

– $\frac{F_2}{F_1} = 1/1 = 1.0$
– $\frac{F_3}{F_2} = 2/1 = 2.0$
– $\frac{F_4}{F_3} = 3/2 = 1.5$
– $\frac{F_5}{F_4} = 5/3 \approx 1.666$
– $\frac{F_6}{F_5} = 8/5 = 1.6$
– $\frac{F_{10}}{F_9} = 55/34 \approx 1.6176$
– $\frac{F_{15}}{F_{14}} = 610/377 \approx 1.6180$

這種收斂現象並非偶然，而是數學結構的必然結果。黃金比例所衍生的「黃金矩形」與「黃金螺旋」，更進一步將抽象數學轉化為視覺上的和諧。黃金螺旋以對數形式向外擴展，每一圈的增長比例皆為 $\phi$，這種曲線不僅美學上令人愉悅，也在自然界中反覆出現。

黃金比例在自然界與藝術中的展現

從微觀到宏觀，黃金比例彷彿是宇宙的設計語言。在植物界，向日葵的種子以兩組反向螺旋排列，其數量往往是相鄰的費波那契數（如34與55，或55與89），這種排列確保種子在有限空間中分布最均勻，最大化生長效率。松果的鱗片、菠蘿的紋路、甚至樹枝分叉的模式，也都遵循相同規律。植物學家認為，這是一種經過演化優化的生長策略，稱為「葉序」（phyllotaxis），能讓每片葉子獲得最多的陽光與空氣。

動物界同樣存在黃金比例的印記。鸚鵡螺的殼體呈現完美的黃金螺旋，每一室的大小按 $\phi$ 比例擴增，既符合結構強度，也體現生長的連續性。蝸牛殼、羊角、甚至颱風的雲系與星系的旋臂，都展現出類似的幾何模式。人類自身也難以逃脫這套數學規律：從臉部五官的間距、手指關節的長度比，到肚臍至腳底與頭頂的距離比例，許多研究指出這些都接近黃金比例，或許解釋了為何人們普遍認為符合此比例的面容更具吸引力。

在藝術與建築領域，黃金比例長期被視為美的準則。古希臘帕德嫩神廟的立面比例、埃及吉薩金字塔的斜面設計，都被認為融入了黃金矩形。文藝復興時期，達文西在《維特魯威人》中精確描繪人體比例，並在《蒙娜麗莎》與《最後的晚餐》的構圖中運用黃金分割，引導觀者視線，創造平衡與和諧。直至今日，設計師在產品外觀、網頁版面、攝影構圖中仍廣泛運用此原則，以提升視覺舒適度。想進一步了解黃金比例的科學與美學意義，可參考 Live Science 對黃金比例的深入探討。

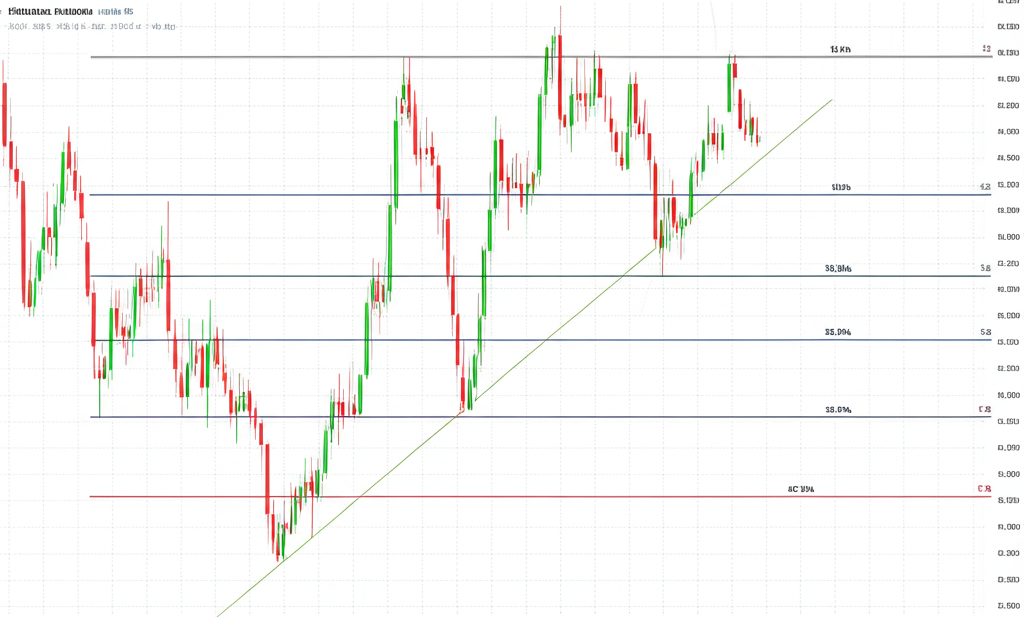
費波那契數列在金融交易中的應用：斐波那契回撤與擴展

在看似混亂的金融市場中，交易者總在尋找能預測價格轉折的工具，而費波那契數列正是技術分析中的重要支柱。透過觀察價格波動的幾何關係，斐波那契回撤（Fibonacci Retracement）與擴展（Fibonacci Extension）提供了客觀的支撐與阻力位參考，幫助投資人判斷趨勢延續或反轉的可能位置。

斐波那契回撤主要用於衡量價格在趨勢中的「修正幅度」。當一段上漲或下跌行情結束後，價格通常不會直接反向，而是先進行調整。交易者利用斐波那契比率來預估這段回調可能停下的位置。這些比率源自數列中相鄰項的比值，最常見的包括：23.6%（由 $F_{n-3}/F_n$ 近似）、38.2%（$F_{n-2}/F_n$）、50%（心理關卡，非嚴格斐波那契）、61.8%（黃金比例的倒數）與78.6%（$\sqrt{61.8\%}$）。其中，38.2%與61.8%被視為關鍵水平，因為它們直接與黃金比例相關。

相對地，斐波那契擴展則用於預測價格突破原有高點或低點後的「延伸目標」。常見擴展比率如127.2%、161.8%（即 $\phi$）與261.8%，這些數值可作為潛在的獲利目標區間。例如，若價格完成一波上漲後回調，再啟動新一波上攻，交易者便可利用擴展工具預估其可能到達的高點。

如何繪製斐波那契回撤線與實戰交易策略

在主流交易平台上，如TradingView，繪製斐波那契回撤線的操作相當直觀：

1. **選定趨勢區間**：在上升趨勢中，將工具的起點（0%）設於最低點，終點（100%）設於最高點；在下降趨勢中則相反。
2. **拖曳生成線段**：啟用斐波那契回撤工具後，從起點拖曳至終點，系統即自動標示出23.6%、38.2%、50%、61.8%等水平線。
3. **觀察價格反應**：這些水平線代表潛在的支撐（上升趨勢回調時）或阻力（下降趨勢反彈時）。

**實戰應用策略**：

– **反轉確認**：當價格接近61.8%或38.2%回撤位，並出現反轉K線型態（如錘子線、吞沒線）或交易量配合，可能代表調整結束，趨勢延續。例如，多頭可在61.8%支撐位附近佈局，止損設於其下方。
– **進出場規劃**：回撤水平可用於設定買進點與停損，擴展水平則用於規劃獲利目標，形成完整交易架構。
– **多重驗證**：單獨使用斐波那契工具風險較高。若回撤位恰好與移動平均線、趨勢線或前波高低點重合，則其有效性大幅提升。搭配RSI、MACD等指標，可進一步確認買賣時機。

進一步了解此工具的實際操作，建議參考 Investopedia 的斐波那契回撤解釋。

斐波那契交易的優勢、局限性與風險管理

**優勢**：

– **客觀參考**：提供明確的數值水平，減少主觀猜測。
– **跨市場通用**：適用於股票、外匯、加密貨幣、期貨等多種資產。
– **群體共識效應**：因大量交易者使用，這些水平往往形成自我實現的預期。

**局限性**：

– **非精確預測**：僅提供機率性參考，價格可能穿透或跳過這些水平。
– **起點主觀**：不同交易者可能選取不同波段，導致分析結果分歧。
– **忽略基本面**：無法反映公司財報、政策變動等實質因素。

**風險管理要點**：

– **嚴設停損**：任何交易都應預先規劃最壞情況下的退出點。
– **資金控管**：單筆交易風險建議不超過總資金的1%~2%。
– **多空驗證**：結合趨勢、動能、量能等多維度訊號，避免孤注一擲。
– **持續檢討**：定期回測策略，適應市場結構變化。

非波那契數列與程式設計：遞迴演算法深度解析

在程式設計教育中，非波那契數列幾乎是每位初學者接觸「遞迴」（Recursion）的起點。遞迴是一種函式呼叫自身的設計模式，適合解決可分解為相似子問題的任務。費波那契的定義 $F_n = F_{n-1} + F_{n-2}$ 天然具備遞迴結構，使其成為教學上的理想範例。

以下為遞迴實作的邏輯示意：

“`
函式 fibonacci(n):
若 n == 0: 回傳 0
若 n == 1: 回傳 1
否則: 回傳 fibonacci(n-1) + fibonacci(n-2)
“`

此寫法簡潔直觀，完全反映數學定義。當計算 `fibonacci(5)` 時，程式會自動分解為 `fibonacci(4)` 與 `fibonacci(3)`，並持續展開，直到抵達 `n=0` 或 `n=1` 的終止條件。然而，這種直覺方法隱藏著嚴重效能問題。

遞迴與迭代實現的比較與效能優化

儘管遞迴寫法優雅，其時間複雜度卻高達 $O(2^n)$，原因在於大量重複計算。例如，`fibonacci(3)` 在計算過程中會被呼叫多次，每一層都重新運算，導致效率急劇下降。此外，深層遞迴會耗盡呼叫堆疊，引發「堆疊溢位」錯誤。

相較之下，迭代法以線性方式逐步計算，效率大幅提升：

“`
函式 fibonacci_iterative(n):
若 n == 0: 回傳 0
若 n == 1: 回傳 1
a = 0, b = 1
對 i 從 2 到 n:
temp = a + b
a = b
b = temp
回傳 b
“`

迭代法僅需 $O(n)$ 時間與 $O(1)$ 空間，實用性遠高於原始遞迴。

為兼顧遞迴的清晰與效率，可引入「記憶化」（Memoization）技術：

“`
函式 fibonacci_memo(n, cache = {}):
若 n 在 cache 中: 回傳 cache[n]
若 n <= 1: 回傳 n cache[n] = fibonacci_memo(n-1, cache) + fibonacci_memo(n-2, cache) 回傳 cache[n] ``` 透過快取已計算結果，時間複雜度降至 $O(n)$，成為學習動態規劃（Dynamic Programming）的經典入門案例。

非波那契數列在日常生活與科技中的其他應用

除了數學與自然，費波那契數列的影響遍及多個領域：

– **音樂創作**：作曲家如巴爾托克與德布西，據信在作品結構中運用費波那契數安排樂段長度或高潮位置，使聽感更富層次與和諧。
– **密碼學**：某些偽隨機數生成器利用費波那契遞推特性，產生難以預測的序列，應用於加密通訊。
– **演算法設計**：費波那契搜尋用於有序陣列的高效查找；費波那契堆則是一種優先佇列資料結構，可優化圖形演算法（如Dijkstra最短路徑）的執行效率。
– **電腦圖形學**：黃金螺旋與費波那契格點常用於生成自然景觀、植物模型或 procedural texture，提升視覺真實感。
– **設計與排版**：現代UI/UX設計師常以黃金比例規劃版面、字型大小與元素間距，創造直覺且美觀的使用者介面。
– **社會科學**：雖具爭議，但有研究嘗試在人口成長曲線或經濟週期中尋找費波那契模式，反映人類對規律的本能追尋。

結論：非波那契數列的深遠影響與無限可能

從中世紀的兔子問題到現代金融與演算法，非波那契數列展現了數學的深遠影響力。它不僅是一串數字，更是一種跨越領域的結構性語言，連結自然法則、人類美學與科技邏輯。無論是葉片的排列、市場的波動，還是程式碼的執行效率，背後都隱藏著這條簡單卻強大的數列。它提醒我們，複雜世界往往建立在極簡規則之上。隨著科學與技術的進步，費波那契數列仍將持續啟發新發現，成為人類理解宇宙秩序的重要途徑之一。